[:it]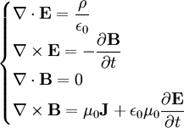
La teoria del campo elettromagnetico è sintetizzata in quattro leggi. Esse sono chiamate equazioni di Maxwell poiché fu Maxwell che, oltre a formulare la quarta legge, comprese che esse costituiscono il fondamento essenziale della teoria delle iterazioni elettromagnetiche.
La prima equazione di maxwell è la legge di Gauss per il campo elettrico.
Oltre che esprimerla in forma integrale:
si può esprimere in forma differenziale.
.
Considerando una variazione infinitesima di campo elettrico lungo una direzione la relazione precedente diventa:
Considerando le tre dimensioni e derivando la relazione iniziale:
si ha:
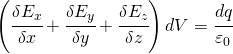
ossia:
con 
densità di carica volumetrica.
In termini matematici si può scrivere:
ossia la divergenza del vettore campo elettrico è uguale alla densità di carica volumetrica divisa la costante dielettrica nel vuoto.[:]